Wolfram Alpha: Il tuo Alleato Perfetto per Analisi 1 e 2

Updated at: 13/07/2025

Analisi 1 e 2 ti mettono a dura prova? Non disperare! Wolfram Alpha è qui per aiutarti. Questo potente strumento online va ben oltre una semplice calcolatrice: risolve equazioni, traccia grafici, semplifica calcoli complessi e fornisce spiegazioni dettagliate. Scopri come Wolfram Alpha può diventare il tuo alleato perfetto per affrontare con successo gli esami e comprendere a fondo i concetti chiave dell'analisi matematica. Preparati a semplificare il tuo studio!

Istruzioni Passo dopo Passo

  1. Accesso a Wolfram Alpha

    • Accedi a Wolfram Alpha (www.wolframalpha.com).
    Accedi a Wolfram Alpha (www.wolframalpha.com).
    Accesso a Wolfram Alpha

  2. Analisi 1: Calcoli di base

    • Utilizza la barra di input 'Mathematica input' e clicca sulla stellina per trovare operatori matematici (limiti, derivate, integrali). Definisci la funzione e la variabile. Premi invio.
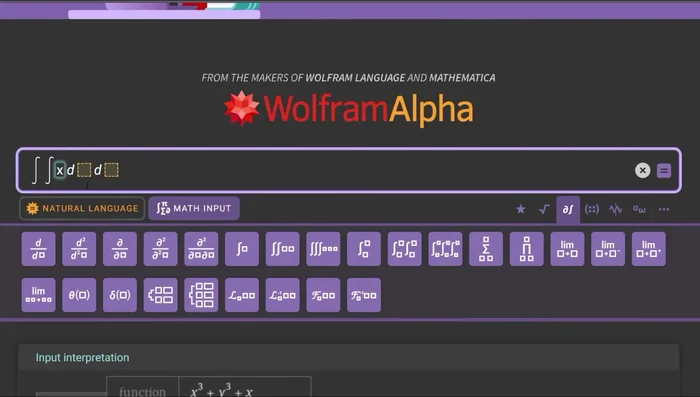
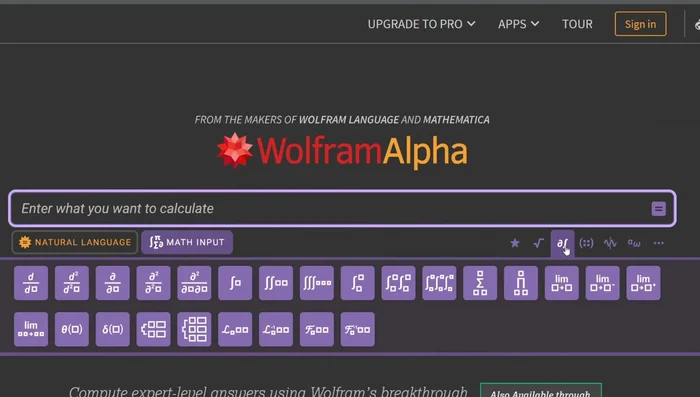
    Per Analisi 1: Utilizza la barra di input 'Mathematica input' e clicca sulla stellina per trovare operatori matematici (limiti, derivate, integrali). Definisci la funzione e la variabile. Premi invio.
    Analisi 1: Calcoli di base

  3. Analisi 1: Richieste qualitative

    • Scrivi comandi come 'Taylor of [funzione]', 'Graph of [funzione]', 'Find Maxima and minima of [funzione]'.
    Per richieste qualitative: Scrivi comandi come 'Taylor of [funzione]', 'Graph of [funzione]', 'Find Maxima and minima of [funzione]'.
    Analisi 1: Richieste qualitative

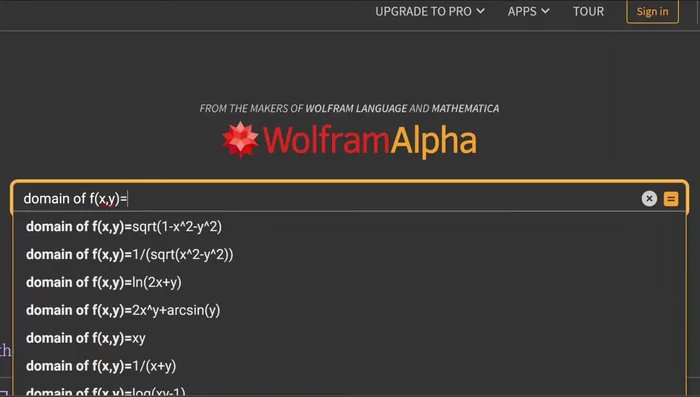
  4. Analisi 2: Studio del Dominio

    • Per studiare il dominio di una funzione in più variabili, scrivi 'Domain of f(x,y)' e inserisci l'espressione algebrica.
    Analisi 2: Per studiare il dominio di una funzione in più variabili, scrivi 'Domain of f(x,y)' e inserisci l'espressione algebrica.
    Analisi 2: Studio del Dominio

  5. Analisi 2: Limiti in due variabili

    • Seleziona il comando appropriato e digita le variabili, a cosa tendono e la funzione.
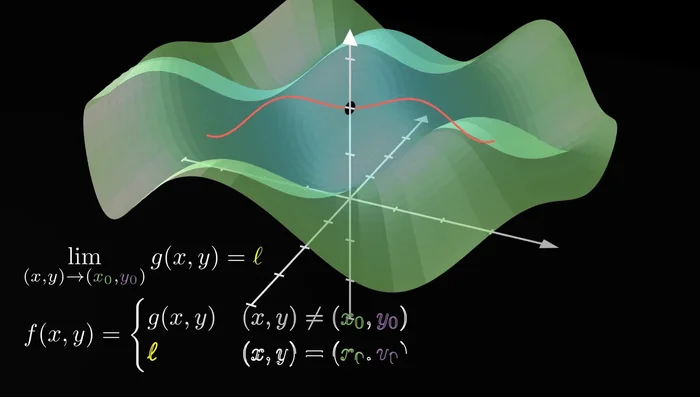
    Limiti in due variabili: Seleziona il comando appropriato e digita le variabili, a cosa tendono e la funzione.
    Analisi 2: Limiti in due variabili

  6. Analisi 2: Continuità, Derivabilità e Differenziabilità

    • Verifica i limiti per la continuità, trasforma la funzione in una variabile per la derivabilità (sostituendo la coordinata del punto), e utilizza la formula della differenziabilità per la differenziabilità.
    Continuità, derivabilità e differenziabilità: Verifica i limiti per la continuità, trasforma la funzione in una variabile per la derivabilità (sostituendo la coordinata del punto), e utilizza la formula della differenziabilità per la differenziabilità.
    Analisi 2: Continuità, Derivabilità e Differenziabilità

  7. Analisi 2: Massimi, Minimi e Punti di Sella

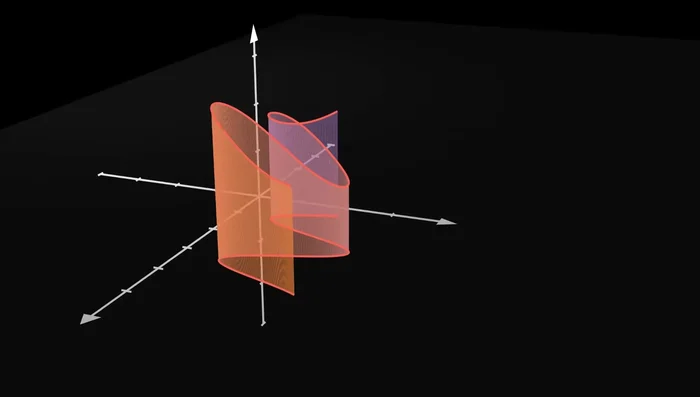
    • Scrivi 'Find Maxima and minima of [funzione]' per trovare punti di massimo, minimo e di sella.
    Massimi e minimi in due variabili: Scrivi 'Find Maxima and minima of [funzione]' per trovare punti di massimo, minimo e di sella.
    Analisi 2: Massimi, Minimi e Punti di Sella

  8. Analisi 2: Integrali Doppi e Tripli

    • Wolfram richiede l'impostazione rigorosa in forma normale. Per domini complessi (es. cerchio), scomponi il dominio in parti più semplici definite da funzioni.
    Integrali doppi e tripli: Wolfram richiede l'impostazione rigorosa in forma normale. Per domini complessi (es. cerchio), scomponi il dominio in parti più semplici definite da funzioni.
    Analisi 2: Integrali Doppi e Tripli

  9. Analisi 2: Integrali Curvilinei e di Superficie

    • Non ci sono comandi diretti. Scomponi l'integrale in una forma più operativa e inseriscilo nella barra di ricerca.
    Integrali curvilinei e di superficie: Non ci sono comandi diretti. Scomponi l'integrale in una forma più operativa e inseriscilo nella barra di ricerca.
    Analisi 2: Integrali Curvilinei e di Superficie

  10. Analisi 2: Campi Vettoriali

    • Trova divergenza e rotore, ma per lavoro e flusso, scomponi gli integrali in forme più semplici.
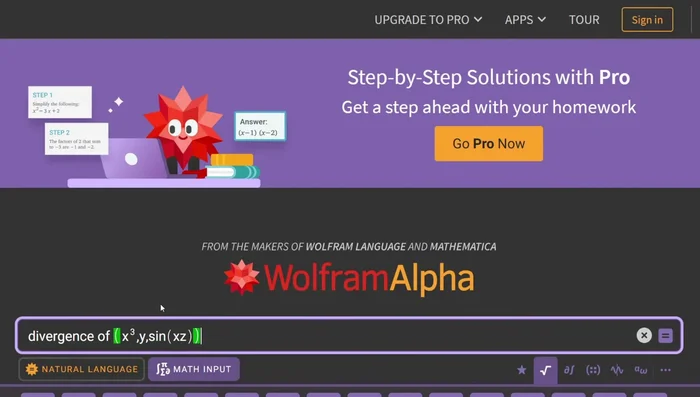
    Campi vettoriali: Trova divergenza e rotore, ma per lavoro e flusso, scomponi gli integrali in forme più semplici.
    Analisi 2: Campi Vettoriali

  11. Analisi 2: Equazioni Differenziali

    • Scrivi l'equazione, usando l'apice per le derivate. Aggiungi le condizioni iniziali con una virgola.
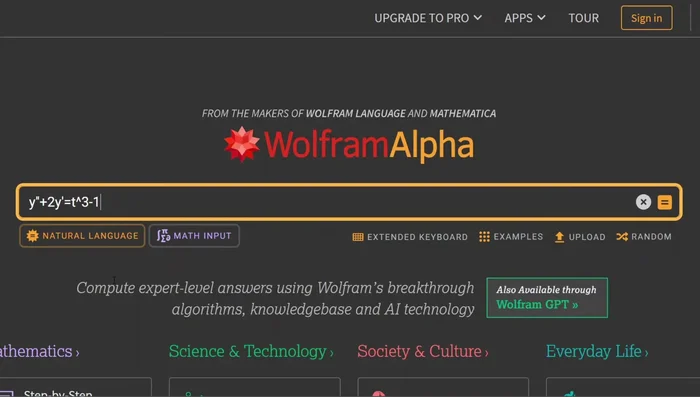
    Equazioni differenziali: Scrivi l'equazione, usando l'apice per le derivate. Aggiungi le condizioni iniziali con una virgola.
    Analisi 2: Equazioni Differenziali
[RelatedPost]

Tips

  • Conoscere la teoria è fondamentale per interpretare correttamente i risultati di Wolfram Alpha.
  • Per problemi complessi, scomponi il problema in parti più gestibili.

Common Mistakes to Avoid

1. Sintassi errata nell'inserimento delle funzioni

Motivo: Wolfram Alpha utilizza una sintassi specifica per le funzioni matematiche. Errori nella scrittura (ad esempio, parentesi mancanti o uso scorretto di operatori) portano a risultati errati o a nessun risultato.
Soluzione: Verificare attentamente la sintassi seguendo le convenzioni di Wolfram Alpha e consultare la documentazione online per eventuali dubbi.

2. Interpretazione errata dei risultati

Motivo: Wolfram Alpha fornisce risultati spesso complessi. Una comprensione superficiale del risultato potrebbe portare a conclusioni errate riguardo a limiti, derivate o integrali.
Soluzione: Analizzare attentamente il risultato fornito, confrontandolo con la teoria studiata e cercando di comprendere il significato matematico di ogni elemento.

FAQs

Wolfram Alpha è gratuito o a pagamento?
Wolfram Alpha offre una versione gratuita con funzionalità base. Per accedere a funzionalità più avanzate e a un utilizzo senza limiti, è disponibile un abbonamento a pagamento (Wolfram Alpha Pro).
Come inserisco correttamente le formule in Wolfram Alpha per Analisi 1 e 2?
Utilizza una notazione matematica standard. Per esempio, per derivare x^2 scrivi 'derivative x^2'. Per integrali, usa 'integrate x^2 dx'. Se hai dubbi, consulta la documentazione di Wolfram Alpha o prova diverse formulazioni fino a ottenere il risultato desiderato. Ricorda di specificare le variabili e gli intervalli di integrazione quando necessario.